Arrhythmia Data Sonification

By Victor Mercola

My father, Mark Mercola, is a professor of medicine at Stanford University and the head of the Mercola Lab (as of writing this project). While talking with him about the classes I take at WPI, he mentioned how it would be interesting to use data sonification to educate and/or demonstrate the effectiveness of a new drug that he is working on. I agreed with his proposal and used the data he gave me for my final project in MU3620, Arrhythmia Data Sonification. Using GNU Octave, Ableton Live, and Sonic Pi, I was able to make "music" that would change according to an arrhythmic heartbeat.

Introduction

Before working with music, there is some important preliminary background information to go over.

The standard heartbeat seen on electrocardiograms (ECG / EKG) and other heart monitors is comprised of five different sections, named the "P Wave", the "QRS Complex", and the "T Wave". The specific disease my father is working on is Long QT syndrome - as its name suggests, Long QT syndrome is a fatal, congenital cardiac rhythm disorder that where the length of the QT interval is longer than usual, causing arrhythmia patterns. My father is specifically working on Long QT type 3 (a.k.a. Long QT3 syndrome), which is caused by a problem regulating sodium ions in heart cells. My father is currently working on a new drug to treat disease, named "Mex2A" and nicknamed "Super Mex" by his staff.

Processing the Data, with GNU Octave

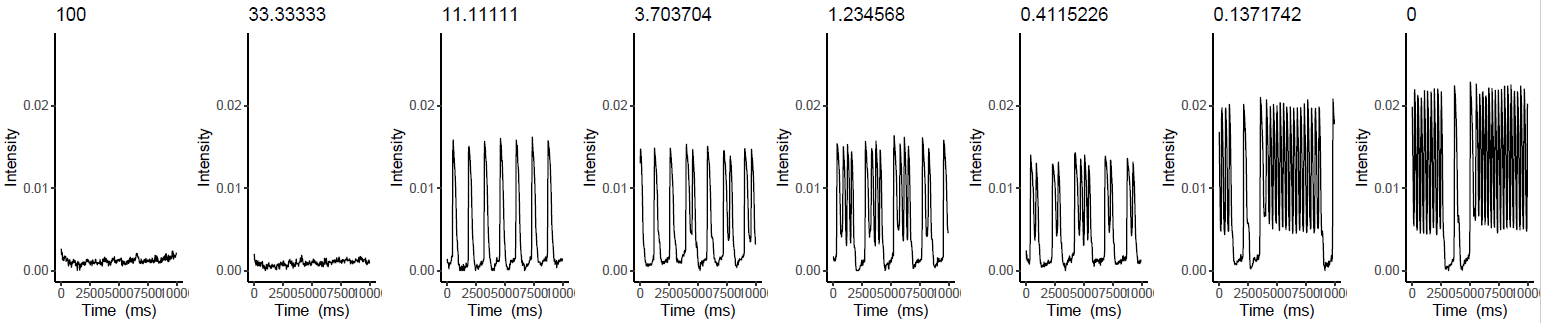
My father sent me a large spreadsheet that, when graphed, produced the results of the graphs above. These show the results of human heart cells with Long QT3 syndrome given different dose amounts of Mex2A, in micromolar. The graphs' X-axes show the measured time in milliseconds, with measured intervals spaced roughly 30 ms apart. The graphs' Y-axes show the measured intensity - when the heart cells beat, the intensity goes up. One can tell from the graphs that the 100uM dose and 33.333uM dose results do not show any peaks, but the 11.111uM dose shows strikingly regular peaks denoting a heartbeat. When I saw this data, I thought would be neat to make "music" where each peak represented a music measure's bar line, and the tempo of the song would increase or decrease depending on how fast or slow the heart cells beat, respectively.

To turn the heartbeat data into music intervals, I first opened the file in GNU Octave (open-source MATLAB alternative). I first wanted to find the average interval of the 11uM dose beats, because I wanted the average interval's corresponding BPM to be scaled to 120 BPM. After recording the timestamps of all of the important peaks, I made a new array of intervals of unit milliseconds. With those intervals, I could convert the intervals' inverse, in Hz (1 cycle per second). I then converted the intervals' Hz to BPM (beats per minute) by multiplying by 60.

I figured out that the heart cells when given the 11uM dose could beat at about 43.885 BPM normally. In music terms, that tempo is the faster end of "grave". I could normalize the interval BPM's by dividing each value by the average. From here, it was rinse and repeat for the other graphs - The interval data for 3.703uM, 1.2345uM, 0.4115uM, 0.1271uM, and 0uM were all normalized with the same 43.885 BPM value.

%{
Octave code for generating music from heartbeats
Victor Mercola
MU 3620
2019-12-09
under Prof. Manzo
%}
  
pkg load signal;
averageInterval = 1367.2; % interval of average heart rate [ms]
averageHz = 1 / (1367.2 / 1000); % beats-per-minute of average heart rate [Hz]
averageBPM = averageHz * 60; % beats-per-minute of average heart rate [Hz]
% disp(averageBPM) 

%{ 
1 beat        1 beat
-----       = ------
1367.2 ms     1.3672 s
%} 

x = csvread("N406K_forMark.csv",1,0); % original file, a csv 

%{
Mex2A_100uM     = transpose(x(:,2)); % Mex2A - 100 uM
Mex2A_33_333uM  = transpose(x(:,3)); % Mex2A - 33.333 uM
Mex2A_11_111uM  = transpose(x(:,4)); % Mex2A - 11.111 uM
Mex2A_3_703uM   = transpose(x(:,5)); % Mex2A - 3.703 uM
Mex2A_1_2345uM  = transpose(x(:,6)); % Mex2A - 1.2345 uM
Mex2A_0_4115uM  = transpose(x(:,7)); % Mex2A - 0.4115 uM
Mex2A_0_1271uM  = transpose(x(:,8)); % Mex2A - 0.1271 uM
Mex2A_0uM       = transpose(x(:,9)); % Mex2A - 0 uM
%} 

t = transpose(x(:,1)); % time array [ms]
Mex2A = [100, 33.333, 11.111, 3.703, 1.2345, 0.4115, 0.1271, 0]; 

n = 3; 

% find the peaks in the graph
this_row = transpose(x(:,n + 1));
[pks idx] = findpeaks(this_row, "MinPeakHeight",0.015, "MinPeakDistance", 5); 

% convert those peak values from findpeaks into coordinates
peakX = t(idx);
peakY = this_row(idx);
disp(peakX);  
 
f = figure;
plot(t, this_row, peakX, peakY, 'x');
axis([min(t), max(t), 0, 0.03]);
title(["Intensity of Mex2A=", num2str(Mex2A(n)), "uM"]);
xlabel("Time, t [ms]");
ylabel("Intensity"); 

% calculate peak intervals
for i = 2:length(peakX)
    pkToPkInterval(i - 1) = peakX(i) - peakX(i-1); % time between intervals [ms]
end

pkToPkHz = 1./(pkToPkInterval / 1000);  % interval frequency [Hz]
pkToPkBPM = pkToPkHz * 60; % interval frequency [BPM]
disp(pkToPkBPM); 

pkToPkRatio = pkToPkBPM / averageBPM

Now that the data was calculated, I moved it from Octave into Sonic Pi.

Playing the data, with Sonic Pi

# Data Sonification with heartbeats
# Victor Mercola - MU 3620
# Prof. Manzo, 2019-12-09

doses = [11.111, 3.703, 1.2345, 0.4115, 0.1271, 0]

dose = 0
6.times do
  if(dose == 0)
    # 11.111 uM dose
    intervals = [1.00371, 1.00371, 1.00371, 1.00371, 0.98189, 1.00371]
    n = 6
  end
  if(dose == 1)
    # 3.703 uM dose
    intervals = [1.1292, 1.0037, 0.98189, 2.5093, 1.0504, 0.98189, 2.5093, 1.0754, 2.3772]
    n = 9
  end
  if(dose == 2)
    # 1.2345 uM dose
    intervals = [2.5093, 3.7639, 3.7639, 1.1581, 2.5093, 3.7639, 3.7639, 1.1292, 2.6569, 3.7639, 3.7639, 1.1292, 2.5093, 1.0504]
    n = 14
  end
  if(dose == 3)
    # 0.4115 uM dose
    intervals = [2.8229, 0.961, 2.8229, 0.94098, 2.8229, 4.1061, 3.7639, 0.961, 3.0111, 0.94098, 2.8229]
    n = 11
  end
  if(dose == 4)
    # 0.1271 uM dose
    intervals = [4.1061, 4.5167, 1.1016, 0.94098, 2.6569, 4.1061, 5.0185, 4.5167, 5.0185, 4.5167, 5.0185, 4.5167, 4.5167, 4.5167, 4.5167, 4.5167, 4.5167, 4.1061, 4.1061, 4.5167, 1.1292]
    n = 21
  end
  if(dose == 5)
    # 0 uM dose
    intervals = [5.0185, 4.5167, 5.0185, 5.0185, 4.5167, 5.0185, 4.5167, 4.5167, 1.1886, 1.0037, 2.6569, 4.5167, 5.0185, 5.0185,  5.6459, 5.0185, 5.0185, 5.0185, 5.0185, 5.0185, 5.0185, 5.0185, 4.5167, 5.0185, 5.0185, 4.5167]
    n = 26
  end
  
  # Here's where the actual music happens
  
  i = 0
  n.times do
    puts(doses[dose],"uM")
    puts(intervals[i])
    sample "D:/OneDrive/Documents/GNU Octave/quick drum loop v2.wav", rate:intervals[i]
    wait 2 * (1 / intervals[i])
    i = i + 1
  end
  
  dose = dose + 1
  wait 1
end

Final Results (and Reception)

The media player is loading...